Finds many (all) roots of one equation within an interval

The function UnirootAll searches the interval from lower to upper for several roots (i.e., zero's) of a function f with respect to its first argument.

UnirootAll(f, interval, lower = min(interval), upper = max(interval),
            tol = .Machine$double.eps^0.5, maxiter = 1000, n = 100, ...)

Arguments

f: the function for which the root is sought.
interval: a vector containing the end-points of the interval to be searched for the root.
lower: the lower end point of the interval to be searched.
upper: the upper end point of the interval to be searched.
tol: the desired accuracy (convergence tolerance).
maxiter: the maximum number of iterations.
n: number of subintervals in which the root is sought.
...: additional named or unnamed arguments to be passed to f (but beware of partial matching to other arguments).

Note

This is a verbatim copy from rootSolve::uniroot.all (v. 1.7).

Value

a vector with the roots found in the interval

Author

Karline Soetaert <karline.soetaert@nioz.nl>

Details

f will be called as f(x, ...) for a numeric value of x.

Run demo(Jacobandroots) for an example of the use of UnirootAll for steady-state analysis.

See also second example of gradient This example is discussed in the book by Soetaert and Herman (2009).

Note

The function calls uniroot, the basic R-function.

It is not guaranteed that all roots will be recovered.

This will depend on n, the number of subintervals in which the interval is divided.

If the function "touches" the X-axis (i.e. the root is a saddle point), then this root will generally not be retrieved. (but chances of this are pretty small).

Whereas unitroot passes values one at a time to the function, UnirootAll passes a vector of values to the function. Therefore f should be written such that it can handle a vector of values. See last example.

Examples

## =======================================================================
##   Mathematical examples
## =======================================================================

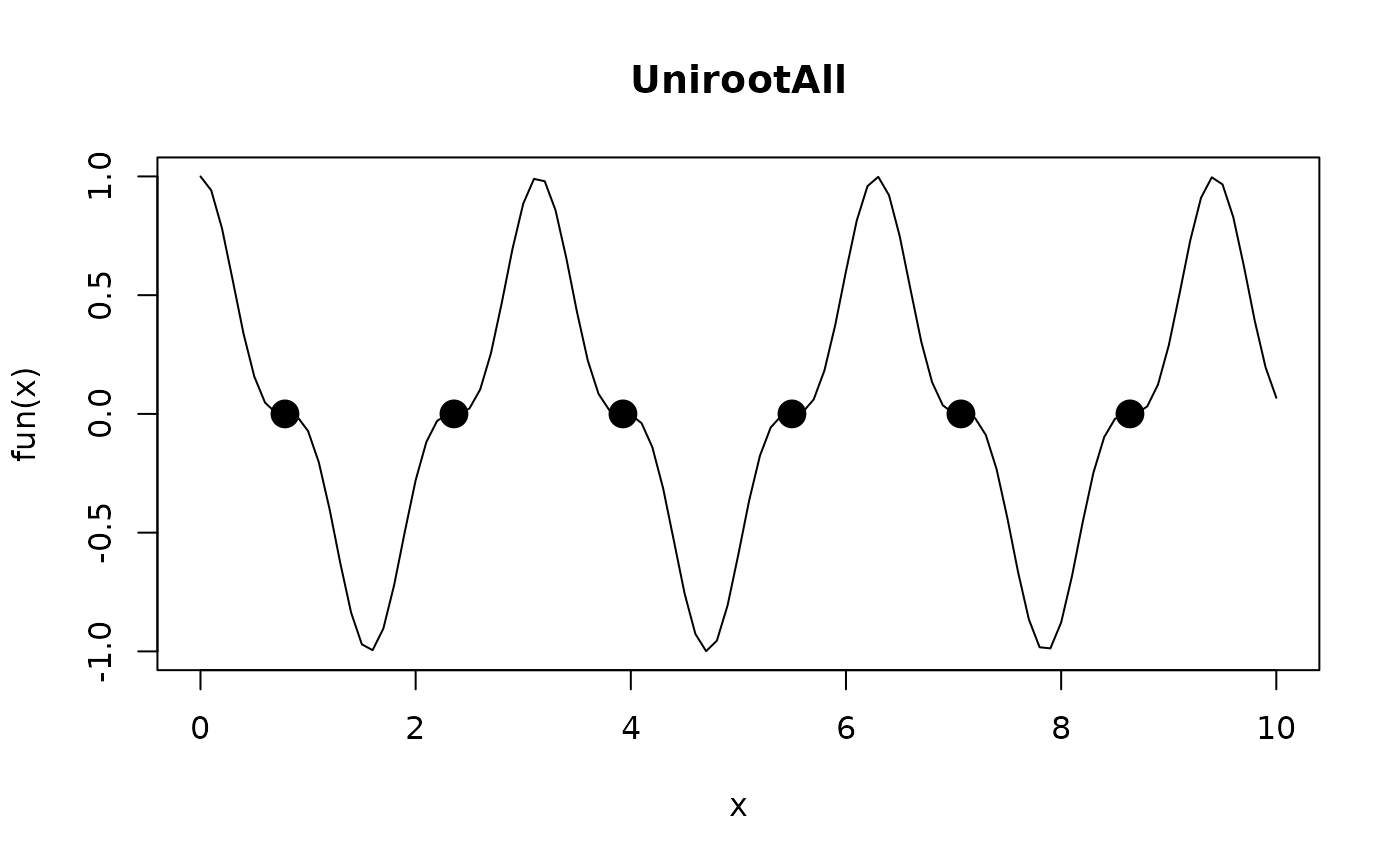
# a well-behaved case...
fun <- function (x) cos(2*x)^3

curve(fun(x), 0, 10,main = "UnirootAll")

All <- UnirootAll(fun, c(0, 10))
points(All, y = rep(0, length(All)), pch = 16, cex = 2)


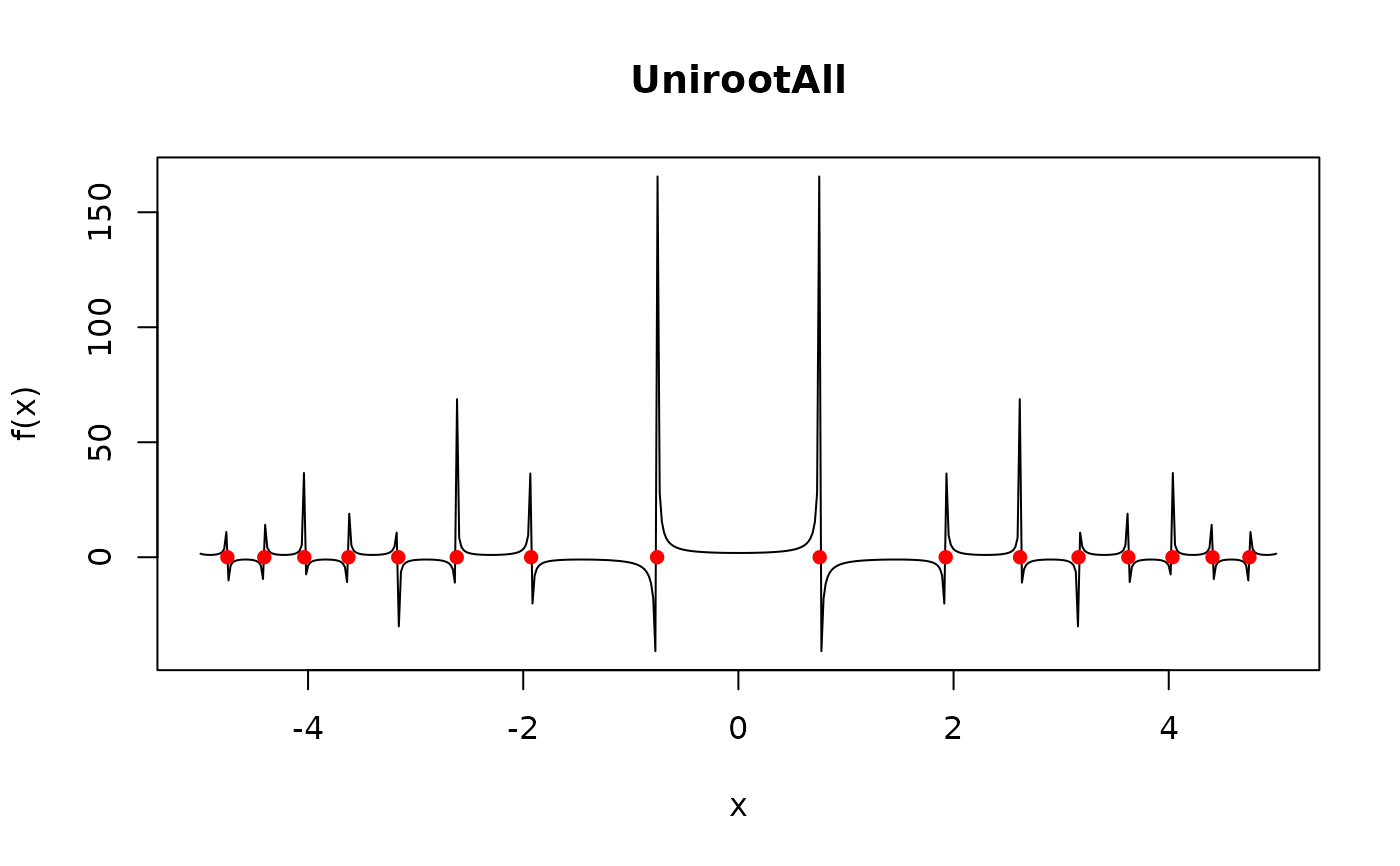
# a difficult case...
f <- function (x) 1/cos(1+x^2)
AA <- UnirootAll(f, c(-5, 5))
curve(f(x), -5, 5, n = 500, main = "UnirootAll")
points(AA, rep(0, length(AA)), col = "red", pch = 16)


f(AA)  # !!!
#>  [1] -19783385  10048135 -17778378  17716401  19705646  21300284 -61531208
#>  [8] -52150718 -52150685 -61531329  21300313  19705621  17716401 -17778378
#> [15]  10048135 -19783436


## =======================================================================
## Vectorisation:
## =======================================================================
# from R-help Digest, Vol 130, Issue 27
# https://stat.ethz.ch/pipermail/r-help/2013-December/364799.html

integrand1 <- function(x) 1/x*dnorm(x)
integrand2 <- function(x) 1/(2*x-50)*dnorm(x)
integrand3 <- function(x, C) 1/(x+C)

res <- function(C) {
  integrate(integrand1, lower = 1, upper = 50)$value +
  integrate(integrand2, lower = 50, upper = 100)$value -
  integrate(integrand3, C = C, lower = 1, upper = 100)$value
}

# uniroot passes one value at a time to the function, so res can be used as such
uniroot(res, c(1, 1000))
#> $root
#> [1] 837
#> 
#> $f.root
#> [1] 0.0000000000162
#> 
#> $iter
#> [1] 9
#> 
#> $init.it
#> [1] NA
#> 
#> $estim.prec
#> [1] 0.000061
#> 

# Need to vectorise the function to use UnirootAll:
res <- Vectorize(res)
UnirootAll(res, c(1,1000))
#> [1] 837