Matrix of Hoeffding's D Statistics

Computes a matrix of Hoeffding's (1948) D statistics for all possible pairs of columns of a matrix. D is a measure of the distance between F(x,y) and G(x)H(y), where F(x,y) is the joint CDF of X and Y, and G and H are marginal CDFs. Missing values are deleted in pairs rather than deleting all rows of x having any missing variables. The D statistic is robust against a wide variety of alternatives to independence, such as non-monotonic relationships. The larger the value of D, the more dependent are X and Y (for many types of dependencies). D used here is 30 times Hoeffding's original D, and ranges from -0.5 to 1.0 if there are no ties in the data. print.HoeffD prints the information derived by HoeffD. The higher the value of D, the more dependent are x and y.

HoeffD(x, y)
# S3 method for class 'HoeffD'
print(x, ...)

Arguments

x

a numeric matrix with at least 5 rows and at least 2 columns (if y is absent), or an object created by HoeffD

y

a numeric vector or matrix which will be concatenated to x

...

ignored

Value

a list with elements D, the matrix of D statistics, n the matrix of number of observations used in analyzing each pair of variables, and P, the asymptotic P-values. Pairs with fewer than 5 non-missing values have the D statistic set to NA. The diagonals of n are the number of non-NAs for the single variable corresponding to that row and column.

Details

Uses midranks in case of ties, as described by Hollander and Wolfe. P-values are approximated by linear interpolation on the table in Hollander and Wolfe, which uses the asymptotically equivalent Blum-Kiefer-Rosenblatt statistic. For P<.0001 or >0.5, P values are computed using a well-fitting linear regression function in log P vs. the test statistic. Ranks (but not bivariate ranks) are computed using efficient algorithms (see reference 3).

Author

Frank Harrell <f.harrell@vanderbilt.edu>
Department of Biostatistics
Vanderbilt University

References

Hoeffding W. (1948) A non-parametric test of independence. Ann Math Stat 19:546–57.

Hollander M., Wolfe D.A. (1973) Nonparametric Statistical Methods, pp. 228–235, 423. New York: Wiley.

Press W.H., Flannery B.P., Teukolsky S.A., Vetterling, W.T. (1988) Numerical Recipes in C Cambridge: Cambridge University Press.

See also

rcorr, varclus

Examples

x <- c(-2, -1, 0, 1, 2)
y <- c(4,   1, 0, 1, 4)
z <- c(1,   2, 3, 4, NA)
q <- c(1,   2, 3, 4, 5)

HoeffD(cbind(x, y, z, q))
#> D
#>   x y z q
#> x 1 0 1 1
#> y 0 1 0 0
#> z 1 0 1 1
#> q 1 0 1 1
#> 
#> avg|F(x,y)-G(x)H(y)|
#>      x    y    z    q
#> x 0.00 0.04 0.16 0.16
#> y 0.04 0.00 0.04 0.04
#> z 0.16 0.04 0.00 0.16
#> q 0.16 0.04 0.16 0.00
#> 
#> max|F(x,y)-G(x)H(y)|
#>      x   y    z    q
#> x 0.00 0.1 0.24 0.24
#> y 0.10 0.0 0.10 0.10
#> z 0.24 0.1 0.00 0.24
#> q 0.24 0.1 0.24 0.00
#> 
#> n= 5 
#> 
#> P
#>   x      y      z      q     
#> x        0.3633 0.0000 0.0000
#> y 0.3633        0.3633 0.3633
#> z 0.0000 0.3633        0.0000
#> q 0.0000 0.3633 0.0000       


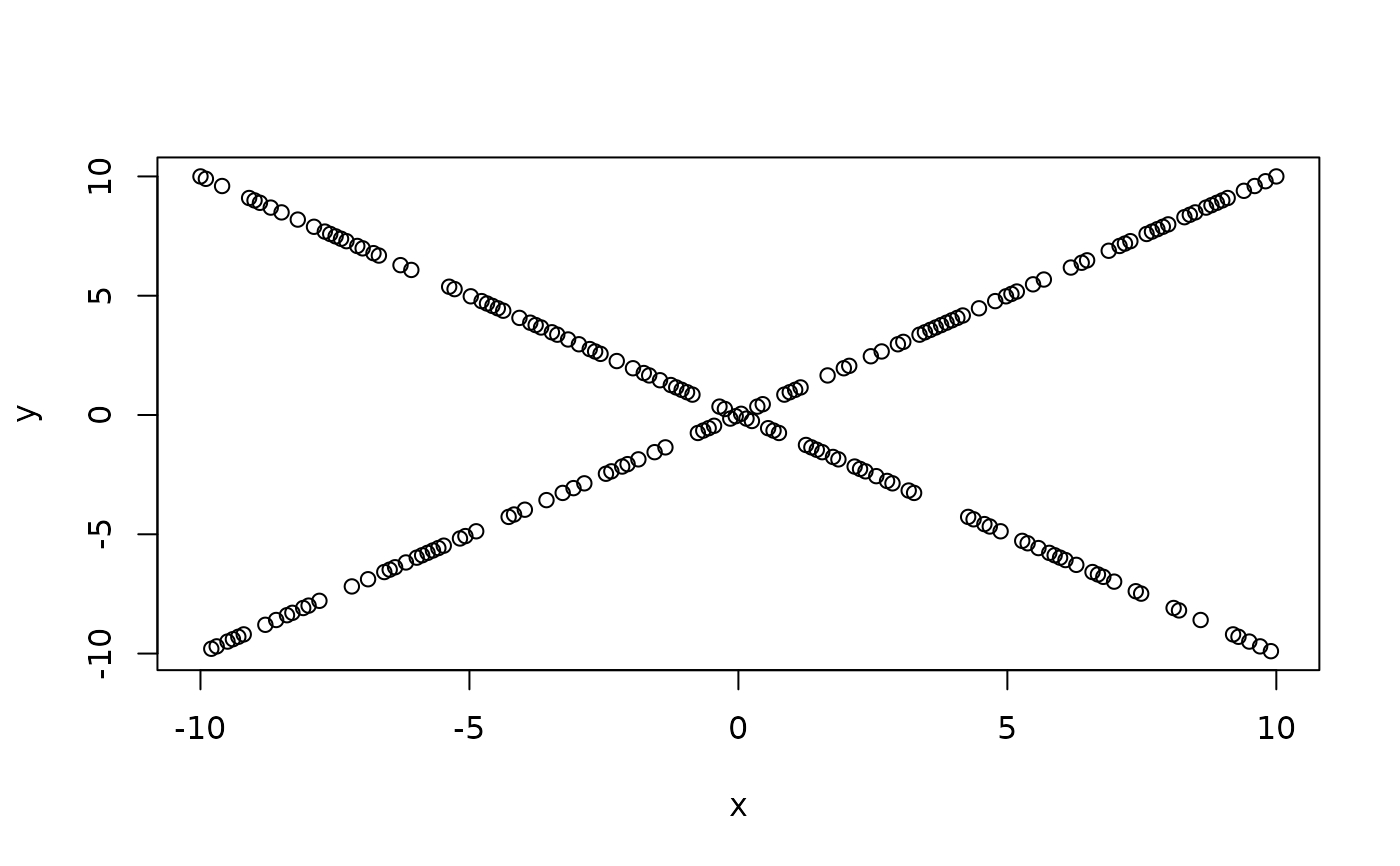
# Hoeffding's test can detect even one-to-many dependency
set.seed(1)
x <- seq(-10, 10, length=200)
y <- x * sign(runif(200, -1, 1))
plot(x, y)


HoeffD(x, y)
#> D
#>      x    y
#> x 1.00 0.06
#> y 0.06 1.00
#> 
#> avg|F(x,y)-G(x)H(y)|
#>        x      y
#> x 0.0000 0.0407
#> y 0.0407 0.0000
#> 
#> max|F(x,y)-G(x)H(y)|
#>        x      y
#> x 0.0000 0.0763
#> y 0.0763 0.0000
#> 
#> n= 200 
#> 
#> P
#>   x  y 
#> x     0
#> y  0