Dunn's Test of Multiple Comparisons

Performs Dunn's test of multiple comparisons using rank sums.

DunnTest(x, ...)

# Default S3 method
DunnTest(x, g,
         method = c("holm", "hochberg", "hommel", "bonferroni", "BH",
                    "BY", "fdr", "none"),
         alternative = c("two.sided", "less", "greater"),
         out.list = TRUE, ...)

# S3 method for class 'formula'
DunnTest(formula, data, subset, na.action, ...)

# S3 method for class 'DunnTest'
print(x, digits = getOption("digits", 3), ...)

Arguments

x: a numeric vector of data values, or a list of numeric data vectors.
g: a vector or factor object giving the group for the corresponding elements of x. Ignored if x is a list.
method: the method for adjusting p-values for multiple comparisons. The function is calling p.adjust and this parameter is directly passed through.
alternative: a character string specifying the alternative hypothesis, must be one of "two.sided" (default), "greater" or "less". You can specify just the initial letter.
out.list: logical, indicating if the results should be printed in list mode or as a square matrix. Default is list (TRUE).
formula: a formula of the form lhs ~ rhs where lhs gives the data values and rhs the corresponding groups.
data: an optional matrix or data frame (or similar: see model.frame) containing the variables in the formula formula. By default the variables are taken from environment(formula).
subset: an optional vector specifying a subset of observations to be used.
na.action: a function which indicates what should happen when the data contain NAs. Defaults to getOption("na.action").
digits: controls the number of fixed digits to print.
...: further arguments to be passed to or from methods.

Details

DunnTest performs the post hoc pairwise multiple comparisons procedure appropriate to follow the rejection of a Kruskal-Wallis test. The Kruskal-Wallis test, being a non-parametric analog of the one-way ANOVA, is an omnibus test of the null hypothesis that none of k groups stochastically dominate one another. Dunn's test is constructed in part by summing jointly ranked data. The rank sum test, itself a non-parametric analog of the unpaired t-test, is possibly intuitive, but inappropriate as a post hoc pairwise test, because (1) it fails to retain the dependent ranking that produced the Kruskal-Wallis test statistic, and (2) it does not incorporate the pooled variance estimate implied by the null hypothesis of the Kruskal-Wallis test.

If x is a list, its elements are taken as the samples to be compared, and hence have to be numeric data vectors. In this case, g is ignored, and one can simply use DunnTest(x) to perform the test. If the samples are not yet contained in a list, use DunnTest(list(x, ...)).

Otherwise, x must be a numeric data vector, and g must be a vector or factor object of the same length as x giving the group for the corresponding elements of x.

Value

A list with class "DunnTest" containing the following components:

res: an array containing the mean rank differencens and the according p-values

Author

Andri Signorell <andri@signorell.net>, the interface is based on R-Core code

References

Dunn, O. J. (1961) Multiple comparisons among means Journal of the American Statistical Association, 56(293):52-64.

Dunn, O. J. (1964) Multiple comparisons using rank sums Technometrics, 6(3):241-252.

Examples

## Hollander & Wolfe (1973), 116.
## Mucociliary efficiency from the rate of removal of dust in normal
##  subjects, subjects with obstructive airway disease, and subjects
##  with asbestosis.
x <- c(2.9, 3.0, 2.5, 2.6, 3.2) # normal subjects
y <- c(3.8, 2.7, 4.0, 2.4)      # with obstructive airway disease
z <- c(2.8, 3.4, 3.7, 2.2, 2.0) # with asbestosis
DunnTest(list(x, y, z))
#> 
#>  Dunn's test of multiple comparisons using rank sums : holm  
#> 
#>     mean.rank.diff   pval    
#> 2-1            1.8 1.0000    
#> 3-1           -0.6 1.0000    
#> 3-2           -2.4 1.0000    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 

## Equivalently,
x <- c(x, y, z)
g <- factor(rep(1:3, c(5, 4, 5)),
            labels = c("Normal subjects",
                       "Subjects with obstructive airway disease",
                       "Subjects with asbestosis"))

# do the kruskal.test first
kruskal.test(x, g)
#> 
#> 	Kruskal-Wallis rank sum test
#> 
#> data:  x and g
#> Kruskal-Wallis chi-squared = 0.77143, df = 2, p-value = 0.68
#> 

# ...and the pairwise test afterwards
DunnTest(x, g)
#> 
#>  Dunn's test of multiple comparisons using rank sums : holm  
#> 
#>                                                                   mean.rank.diff
#> Subjects with obstructive airway disease-Normal subjects                     1.8
#> Subjects with asbestosis-Normal subjects                                    -0.6
#> Subjects with asbestosis-Subjects with obstructive airway disease           -2.4
#>                                                                     pval    
#> Subjects with obstructive airway disease-Normal subjects          1.0000    
#> Subjects with asbestosis-Normal subjects                          1.0000    
#> Subjects with asbestosis-Subjects with obstructive airway disease 1.0000    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 

## Formula interface.
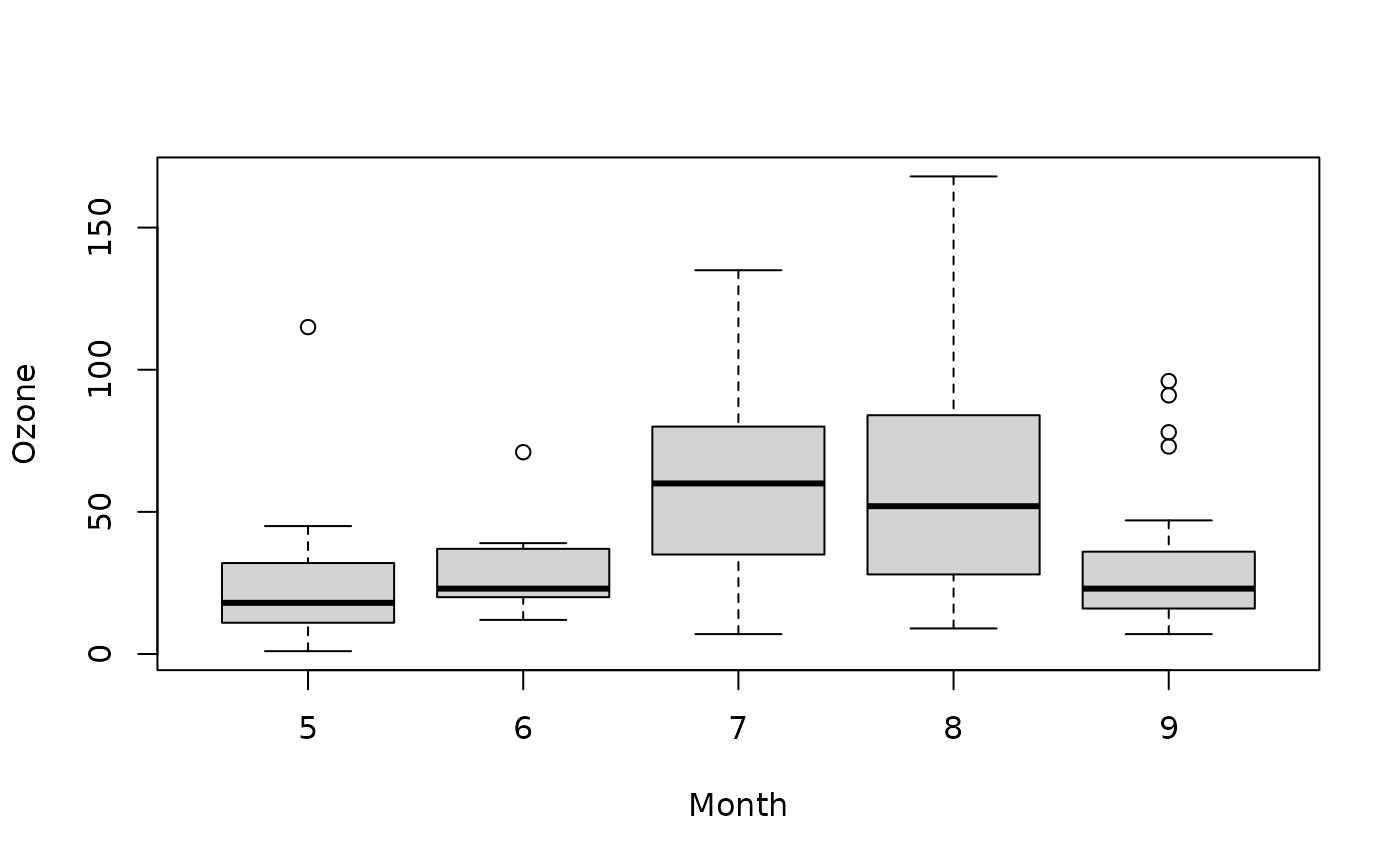
boxplot(Ozone ~ Month, data = airquality)

DunnTest(Ozone ~ Month, data = airquality)
#> 
#>  Dunn's test of multiple comparisons using rank sums : holm  
#> 
#>     mean.rank.diff     pval    
#> 6-5    12.02991453  1.00000    
#> 7-5    41.21153846 0.000099 ***
#> 8-5    38.53846154  0.00032 ***
#> 9-5    11.99734748  0.74574    
#> 7-6    29.18162393  0.14891    
#> 8-6    26.50854701  0.20743    
#> 9-6    -0.03256705  1.00000    
#> 8-7    -2.67307692  1.00000    
#> 9-7   -29.21419098  0.01036 *  
#> 9-8   -26.54111406  0.02428 *  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>